pid控制中三個參數的功能-tft每日頭條

pid控制中三個參數的功能

科技更新时间:2024-05-10 18:30:25

在自動控制中，PID（Proportion-Integrationi-Differentiation:比例-積分-微分）控制算法在近一個多世紀以來在空城控制領域中占據了主導地位。它是由蘇聯工程師Minorsky在1922年在研究艦船自動控制李玲分析中提示的算法。

PID控制算法是通過受控對象的實際行為和目标之間的誤差，通過比例-微分-積分運算再重新作用在被控對象。

pid控制中三個參數的功能（動态演示PID三個參數的作用）1

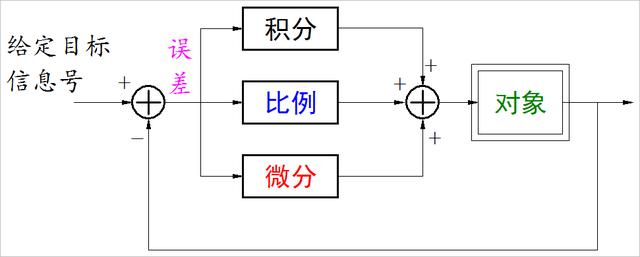
▲ PID控制算法

在工業控制中，PID控制器可以通過模拟、數字方式實現。如今工業應用中的98%以上的過程控制、95%以上的運動控制還都是用這PID控制算法。

對于初學者，掌握PID控制算法參數調整非常重要。下面是來自于公衆号“芯片之家”中的一個推文，其中使用了一個視頻來演示了PID控制在位置跟蹤系統中的應用。

位置跟蹤系統的控制對象是驅動直流電機的電壓，經過電機旋轉帶動機械運動。

pid控制中三個參數的功能（動态演示PID三個參數的作用）2

▲ 一個位置跟蹤PID控制系統

将驅動電機進行簡化，考慮它的轉速與施加電壓成正比，因此轉動角度位置就是轉速的積分。所以對象是一個一階積分慣性系統。

使用普通的比例控制就可以完成無誤差跟蹤随着比例系數增加，跟蹤速度也會提高，但是也會出現過沖震蕩現象。

pid控制中三個參數的功能（動态演示PID三個參數的作用）3

▲ 隻使用比例控制的情況

加入位置的微分（也就是轉速）項可以消除震蕩。如果微分項過大，會使得位置跟蹤變緩慢。特别由于靜摩擦力的存在，有可能會使得位置跟蹤出現小的偏差。

pid控制中三個參數的功能（動态演示PID三個參數的作用）4

▲ 加入微分項，可以消除震蕩

加入積分項，可以将由于系統的靜态摩擦所産生的位置偏差徹底消除。但也會增加系統的震蕩傾向。

所以此時需要綜合調整積分、微分的比例系數。

pid控制中三個參數的功能（動态演示PID三個參數的作用）5

▲ 隻使用I,D控制的效果

綜合調整PID的系數，可以使得系統跟蹤既快又穩。

在很多教科書中也會給出一定的調整順序，或者給出通過系統的單位階躍響應曲線來定量計算最優的PID參數方法。

pid控制中三個參數的功能（動态演示PID三個參數的作用）6

▲ 綜合利用PID達到快速穩定的效果

了解到PID參數與系統誤差之間的物理聯系，是實際中應用PID調節的重要環節。

pid控制中三個參數的功能（動态演示PID三個參數的作用）7

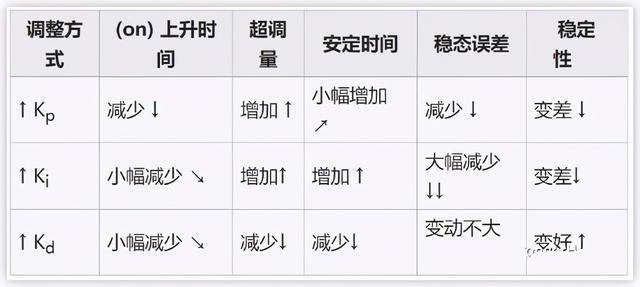
▲ PID控制效果

更多精彩资讯请关注tft每日頭條，我们将持续为您更新最新资讯!

查看全部

网友关注

科技迷你世界食物系統改版
《迷你世界》1.0版本真的很好玩，官方新增了火山地形以及空島，兩個地方風格迥異，火山比較危險，那裡還隐藏着強大的BOSS虛空幻影，而空島則比較漂亮，整個島嶼就是一座座美麗的風景區，玩家可以在島上開采礦物，也可以去尋找星站碎片，這些都是激活星... 2023-01-17
科技華為手機如何一鍵雙系統切換
大家現在應該對重裝系統比較熟悉了吧，那麼您知道計算機可以安裝雙系統嗎？最近，一些網友問自己已經安裝了雙系統，但是啟動的仍然是原始系統，我不知道如何切換雙系統。小編專門來幫助您解除疑問，并帶您了解計算機中的雙系統切換。1.按“winr”鍵打開... 2022-11-24
科技電腦黑屏機箱能亮鼠标鍵盤不能亮
電腦黑屏機箱能亮鼠标鍵盤不能亮?1.檢查顯示器與電腦的連接線是否安裝緊密，建議重新撥插這根連接數據線,或者更換數據線，我來為大家科普一下關于電腦黑屏機箱能亮鼠标鍵盤不能亮?以下内容希望對你有幫助!電腦黑屏機箱能亮鼠标鍵盤不能亮1.檢查顯示器... 2022-12-19
科技最強反套路系統漫畫349
, 2022-12-27
科技筆記本電腦可以跟電視無線投屏嗎
您的會議室是否還在面臨着如下問題：商務辦公會議應用時,如何快速便捷得将筆記本電腦畫面通過無線的方式投屏在顯示終端上顯示,可以說是每家公司都要面臨的一個問題,按照傳統會議模式,您的會議室每次會議都需要花大量的時間提前準備,想要把筆記本電腦或手... 2022-11-29
科技 airpodspro安卓模式調整
【引子】全球第一款藍牙耳機是愛立信公司于1999年在Comdex大展上發布的HBH-10，之後在漫長的歲月中，不斷進化最終演變出了單聲道、立體聲、頸挂式、頭戴式、運行型等多種多樣的産品形态，直到2016年9月蘋果公司發布了第一代AirPod... 2022-12-29
科技光電效應應用原理
導讀：什麼是光電效應？光電效應在實際中有哪些應用？這些應用的原理是什麼？正文什麼是光電效應：當光束照射在金屬表面時，使電子從金屬中脫出的現象，叫做光電效應。光束中存在光子，金屬中存在電子，當光束照射在金屬表面的時候，自然光子也就打在了電子上... 2023-01-07
科技電腦怎麼查詢已經連接的wifi密碼
電腦怎麼查詢已經連接的wifi密碼?忘記wifi密碼怎麼辦，用這招可以知道電腦中的wifi密碼，下面我們就來聊聊關于電腦怎麼查詢已經連接的wifi密碼?接下來我們就一起去了解一下吧!電腦怎麼查詢已經連接的wifi密碼忘記wifi密碼怎麼辦，... 2022-10-13
科技 ip68防水有什麼缺點
ip68防水有什麼缺點?說起IP68級防水防塵等級，相信許多對手機圈有了解的小夥伴應該都不陌生了，如今也有不少旗艦級機型都标配IP68級防塵防水畢竟，大家的用機環境也難免會遇到不小心掉進水裡的情況，如果不具備出色的防水性能，手機分分鐘就得面... 2022-10-08
科技新人做自媒體必備的3個工具網站
互聯網時代幾乎人人都會接觸到自媒體，很多新入門做自媒體的朋友，在從0到1這個階段會存在很多問題，大多數人不知道去哪裡找素材，導緻創作時間長，效率低下。今天這篇文章就跟你分享5個自媒體常用工具，百萬博主同款，付費級分享，建議收藏。01寫标題神... 2023-01-11
科技公共wifi熱點連接上但上不了網
閑暇的休憩時光必然少不了WiFi的陪伴看電影、打遊戲等都離不開網絡可是有時明明信号滿格的WiFi卻連不上網絡，這究竟是怎麼回事呢？快一起來看看吧！來源：新華社責任編輯：馬甯上海星韻内蒙古分公司聯合運營合作熱線：15024793101投稿▏運... 2023-03-16
科技怎麼用u盤安裝電腦系統步驟圖解
怎麼做win10系統u盤，新毛桃迄今已經推出了多個版本。現在，新毛桃win10pe裝機版u盤啟動盤制作工具也已經正式發布了!為了感謝用戶的支持，新毛桃小編就來為大家講解這最新的裝機版u盤啟動盤的整個制作過程。制作裝機版u盤啟動盤準備工作：1... 2023-02-10
科技造夢西遊4手機版年獸技能屬性介紹
朱電金翼衫是造夢西遊4手機版遊戲中沙僧使用的50級橙裝，下面繼續由97973小編為大家帶來關于它的具體屬性以及掉落地點的詳細介紹，想知道的小夥伴趕快來看看吧！朱電金翼衫描述鳳皇翼其承旂兮，高翺翔之翼翼使用角色沙僧50級橙裝獲得方式琉璃宮關卡... 2022-12-04
科技二手小米手機怎麼更換賬戶
我們在某寶，某多，某魚買二手小米手機時，發現有些手機很貴，有些很便宜，為什麼了？搜索了下，才知道便宜的手機基本上是沒解鎖的，沒解鎖就很難刷機，作為刷機愛好者，不能刷機怎麼行？最近就是在研究怎麼刷機改串，改串軟件基本上收費，好不容易找了一款可... 2023-01-31
科技窗台貼大理石方法
窗台貼大理石方法?安裝前需把要用的材料和工具裝備好，需要裝備大理石窗台闆、鋸石機、電焊機以及尺闆等工具，下面我們就來說一說關于窗台貼大理石方法?我們一起去了解并探讨一下這個問題吧!窗台貼大理石方法安裝前需把要用的材料和工具裝備好，需要裝備大... 2022-06-04
科技新版電腦都不能裝win7嗎
小編在給一些客戶的新筆記本重裝系統的時候，有很多人想要回win7系統，都說不習慣用Win10,。因為目前出廠的筆記本預裝的是win10系統，查看一下是英特爾6代以上的配置，這種情況的筆記本是不支持安裝win7系統的。所以對于想要用Win7，... 2023-03-10
科技白金ace16.1欣賞
大家好，今天由胖子小編帶來的【虛測評】18Ksuper積木K136（one77）#本産品基本信息1顆粒數（pcs）22682人仔數（個）03動态組0（可另購）4燈光組0（可另購）5上市時間2021年8月之前18K發了一台TiffanyBlu... 2023-03-16
科技長虹空調怎麼選擇
炎夏已經來臨，熱成狗的你，也有另一種享受。有什麼比蓋着被子吹空調，手裡捧個大西瓜更享受的事了嘛！進入炎夏前，我做的第一件事就是換一個新空調，原先用的是立式空調，最近又添置了一個跑步機，客廳一下子就塞滿了。再加上原先的空調用了好幾年了，幹脆直... 2022-11-17
科技華為兒童模式教程
近日極果發布的一份2020年度家庭教育支出的報告，引發了大家對于家庭教育投入與在線教育日趨提升的重要性的熱議。首先在家庭教育投入方面，有26%的家庭孩子教育投入占家庭年收入的比重超過了50%。拿出一半的家庭收入用于培養孩子，可見“望子成龍”... 2023-02-05
科技 linux常見文件系統
linux常見文件系統?Linux以樹狀結構管理所有目錄、文件，其他分區挂接在某個目錄上，這個目錄被稱為挂接點或安裝點，然後就可以通過這個目錄來訪問這個分區上的文件了比如根文件系統被挂接在根目錄“/”上後，在根目錄下就有根文件系統的各個目錄... 2022-10-17
科技魔獸世界9.0經典技能回歸
NGA版本預測第一人。4月20日淩晨，随着《魔獸世界》新版本發布會塵埃落定，10.0版本正式确定為“巨龍時代”。這是魔獸自4.0大災變版本後再次講述五色巨龍之間的故事。随着新資料片内容的披露，國内最大的魔獸社區NGA論壇也掀起一股讨論熱潮—... 2023-01-15
科技上網需要人臉識别嗎
為有效開展“迎接十九大忠誠保平安跨越式發展鐵警勇争先”主題教育實踐活動，深化“放管服”工作，進一步提高網安部門的便民服務效能，甯洱縣公安局網絡安全保衛大隊積極組織轄區網吧召開“實名寶”人臉識别系統安裝工作宣傳會，并于6月9日至13日完成了全... 2022-11-14
科技豆瓣9分以上韓國電影
親情永遠是世界上最珍貴的東西，簡單直白的說，就是父母。父母給予我們生命，幫助我們成長，是我們人生道路上的第一位啟蒙老師，可以說父母很大程度上就決定了我們一小部分人生。最近，小站在西瓜視頻上發現了一部電影，是2010年的一部韓國片，主要講述母... 2022-11-29
科技 9款遮瑕測評這四款最值得買
最開始化妝的時候，我幾乎都不會太在意遮瑕這方面！但随着現在經常熬夜爆痘，于是也開始逐漸重視起遮瑕來了！現在對于遮瑕方面我還是比較了解滴~ipsa三色遮瑕這一款的遮瑕力度不錯，三個顔色的色調都還是蠻相近的，隻要不是什麼特别大的瑕疵問題，基本上... 2022-12-08
科技換新顯卡後指示燈閃爍無法開機
随着虛拟貨币水漲船高，顯卡一卡難求，多少臭打遊戲的奔走哭号而一卡不可得，或者裝新機用舊卡的情況比比皆是。那麼問題來了，新機配老卡，如同老夫少妻，這拔下插上間總歸不能琴瑟和鳴、水乳交融，出點靈異的問題在所難免。本主碰到的新電腦老顯卡開機不顯示... 2023-01-09
科技成都車牌選号12123流程
今天，記者從市交管局車管所獲悉，從9月18日（下周一）起，我市将正式啟用全國統一機動車号牌選号系統。市民可以通過手機APP“交管12123”、交通安全綜合服務管理平台、公安窗口三種方式選号，市民在選擇号牌将更加方便，選擇也将更多。特别提醒如... 2023-01-12
科技電腦打字指法怎麼練習
電腦打字指法怎麼練習?标準指法是将雙手按照下圖的位置放在鍵盤上，即讓你的左手食指放在字母F上（F鍵上有一個小突起，通常稱之為盲打坐标），右手食指放在字母J上（J鍵也是盲打坐标）然後将雙手的四指并排對齊分别放在相鄰的鍵鈕上，這就是标準指法的位... 2022-06-06
科技 win7無法拖動文件
在計算機的使用過程中，經常會出現在一些突發的狀況，之前就有過這樣的經曆，Win7系統中鼠标無法拖動文件，無法把一個或者多個文件拖到另外的位置，就更别說使用拖動的方式來進行複制了！強制使用刷新也沒用，但是鼠标其它操作都是正常的，一時間感覺整個... 2022-12-10
科技 gps地面監控系統的組成
gps地面監控系統的組成?1.目的為加強行車安全管理，正确運用GPS監控系統對營運車輛的運行狀況實施動态監控，及時糾正和制止違法違規駕駛行為，預防和減少道路交通事故的發生，特制定本制度，今天小編就來聊一聊關于gps地面監控系統的組成?接下來... 2023-01-11
科技為什麼熱天手機掉電快
為什麼熱天手機掉電快?1、去掉手機保護殼，通過觸摸背部位置，判定是在哪裡發熱比較大，是電池還是手機電路闆上如果是電池發熱，也有可能電池已經開始有問題了；部分情況下，電池起脹的時候就要更加注意；而如果用電量下滑有時很快、有時很慢，那麼電池也産... 2023-02-23

tft每日頭條

> 科技

> pid控制中三個參數的功能

pid控制中三個參數的功能

相关科技资讯推荐

热门科技资讯推荐

网友关注