在數字信号處理領域，常遇到需要将一個正整數向上圓整為2的n次方的數據的情況，如對采集到的時域信号做頻譜分析時，常要求數據點數必須滿足為2的n次方，滿足此種情況才可用傅裡葉變換的基2快速算法，以達到較好的運算速度。換句話說，數據點數必須圓整為形如128、512、1024、4096等類型的數字。
那麼，在C/C 語言中，怎樣快速實現這個功能呢？假定給一個正整數x，寫一個函數numTo2N，得到将其向上圓整為2的n次方的值y，下面給出幾種常用方法的C/C 語言代碼實現。
方法1思路：最直接的思維方式，在while循環裡将正整數x始終除以2，直到x除以2的值小于2，統計循環的次數i，若最後x除以2的值大于1，則循環次數i=i 1，返回2的i次方，即是y的值。實現代碼如下：
思路：同方法1類似，給一個初始值i=1，同樣在while循環裡将正整數x右移1位（相當于除以2，隻是舍棄了小數部分），直到x右移1位的值為0，同時，将i左移1位（相當于乘以2），最後，判斷i的值，若是小于原始的x值，則返回i再左移1位的值，否則返回i的值，即是y的值。實現代碼如下：
思路：将給定的數x，表示為2的次方的形式，求解次方的值，将次方向上取整為n值，返回2的n次方的值，即是要求的y值，數學推導如下：
實現代碼如下：
調用上面3個函數，測試代碼如下：
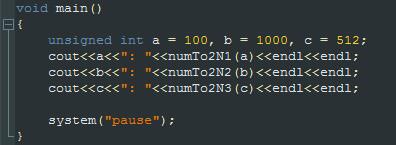
運行結果如下：
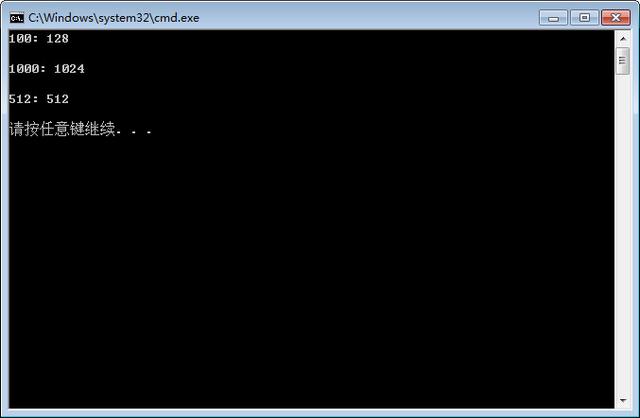
上面3種方法都可以實現我們想要的結果，其中，第1種最直觀，第2種采用移位運算，運行速度最快，第3種涉及到對數的運算，運行速度最慢。
另外，在這個題目的基礎上，可以進一步思考另一個問題，怎樣快速判斷一個數是否為2的n次方？
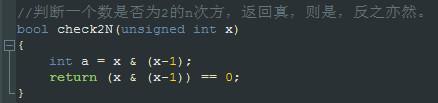
實際上很簡單，如果一個數是2的n次方的話，二進制表示最高位一定是1，其它位是0，如對于數值x=16，其二進制表示為“10000”，則x-1=15，其二進制表示為“01111”，所以x與x-1位與運算為0，而對于不是2的n次方表示的數值，則不滿足這個特點，根據這個思路，可寫下面的函數進行判斷一個數是否為2的n次方：
歡迎加關注，共同交流。
,更多精彩资讯请关注tft每日頭條，我们将持续为您更新最新资讯!
zpostcode 
Recruit 
weather 
mreligion 
Yellowpages 
sport 
constellation 
shopping 
name 
game 
directory 
literature 
Word 
tour 
furnish 
Lottery 
tftnews 
lyrics 
News 
digital 
car 
dir 
Edu 
Finance 
