一、函數的零點：

1、定義：一般地，如果函數 y = f ( x ) 在實數 a 處的值等于零 f ( a ) = 0 ，則 a 叫做這個函數的零點。

對于任意函數，隻要它的圖像是連續不間斷的，其函數的零點具有下列性質：

① 當它通過零點（不是偶次零點）時函數值變号；

② 相鄰兩個零點之間的所有的所有函數值保持同号。

2、函數零點個數的确定方法：

① 判斷二次函數的零點個數一般由判别式的情況完成；

② 對于二次函數在某個閉區間上零點的個數以及不能用判别式判斷的二次函數的零點，則要結合二次函數的圖像進行；

③ 對于一般函數零點的個數的判斷問題不僅要在閉區間 [a , b] 上是連續不間斷的，且f(a) · f（b）＜0，還必須結合函數的圖像和性質才能确定。

函數有多少個零點就是其對應的方程有多少個實數解。

二、典型例題

1、求函數的零點

例題1、 求函數 y＝x^3－x^2－4x＋4 的零點 。

例題3圖（1）

由 ： f ( 0 ) > 0 , 得 2k - 1 > 0 ； f ( 1 ) < 0 , 得 1 k -2 2k - 1 < 0 ； f ( 2) > 0 , 得 4 2(k - 2) 2k - 1 > 0 ；

解得：1/2 < K < 2/3 ∴ 實數 k 的取值範圍是 [ 1/2 , 2/3 ] 。

三、拓展提高

1、已知 f(x) 是定義在R上的奇函數，當 x ≥ 0 時，f(x)＝x^2－3x, 則函數g(x)＝f(x)－x＋3的零點的集合為 ( D )

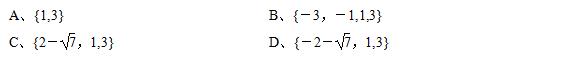
第1題圖

2、已知 x＝－1是函數 f(x)＝a/x ＋b (a≠0) 的一個零點，則函數 g(x)＝ax^2－bx 的零點是 ( C )

A、－1 或 1 B、0 或－1 C、1 或 0 D、2 或 1

3、三次方程x^3＋x^2－2x－1＝0 的根不可能所在的區間為 ( C )

A、(－2，-1) B、(－1,0) C、(0,1) D、(1,2)

4、若函數 f(x) 在定義域 {x|x≠0} 上是偶函數，且在(0，＋∞)上是減函數，f(2)＝0，則函數f(x)的零點有( B )

A、一個 B、兩個 C、至少兩個 D、無法判斷

5、若關于 x 的方程ax^2＋bx＋c＝0(a≠0)有兩個實根1、2，則函數 f(x)＝cx^2＋bx＋a 的零點為( C )

A、1 , 2 B、－1，－2 C、 1，1/2 D、－1，－1/2

6、 已知函數f(x)＝ax^3－2ax＋3a－4 在區間 (－1,1) 上有一個零點 ，求實數 a 的取值範圍 。

答案：1 < a < 2 。

歡迎關注頭條号“尚老師數學”！

更多精彩资讯请关注tft每日頭條，我们将持续为您更新最新资讯!