近代數學在提出無窮學說之後，果然像希臘人擔心的那樣，在數學界引起了混亂，令數學家煩惱不已。這種混亂一直延續着，直到1821年柯西點明了其中的關鍵。

那麼首先回顧一下，無窮引起了什麼樣的怪事。

比方說考慮以下這個無窮級數：

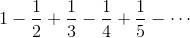
假設求這個無窮級數和的人是想用歸納相鄰項的方法進行計算。

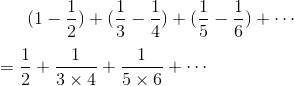
計算這個無窮級數的和是困難的，但明顯看出和是比1/2大的數。可是如果一個人稍微偷點懶，像下式那樣計算，答案則為0。方法是漂亮的，假如這個人把加法和減法各自分開計算：

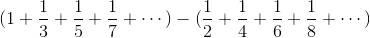
上式加上

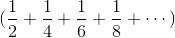
再減去同樣的項，答案應該是不變的。所以答案等于

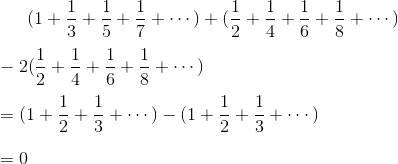
這個狡猾的人得出的答案是0，到底哪個答案是正确的呢？想來想去似乎二者都正确。

下面舉出捷克的哲學家波爾察諾（1781-1848）所著《無窮悖論》一書裡寫的例子。

那個例子是1和-1交替出現的級數（波爾察諾級數），即

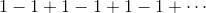
為了計算這個級數，有三個人采用了三種不同的方法進行計算，結果得出三種不同的答案。

第一個人從開始就進行相鄰兩數的歸納計算，答案是0。

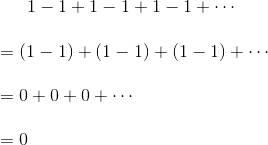
第二個人從第二個數開始再進行相鄰兩數的歸納計算，答案是1。

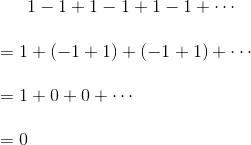
可是第三個人用代數方法，把未知數作為x來計算，答案是1/2。

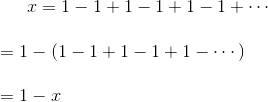
結果x=1-x，解這個方程，則

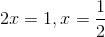
最先得出這個1/2答案的人比波爾察諾要早100年，是名叫格蘭第（1671-1742）的意大利人。

他用下述牽強附會的理由解釋答案為什麼是1/2。父親給兩個兒子留下一塊寶石，可是一塊寶石不能分開，于是決定兄弟倆一年換一次，輪流保存這塊寶石，結果就是兩人都有1/2塊寶石一樣。

沒有答案的加法

這個叫無窮的怪物，雖然不斷地破壞以往的一些知識，但是一段時間内，誰都願意馴養這個怪物，這對數學的發展是否有好處呢？

柯西第一個創立了無窮級數的正确理論。由于這一點柯西建立了不朽的功績，盡管他的着眼點多少有點像哥倫布立雞蛋的故事，他敏銳地發現了他以前的數學家沒有發現的兩點，其中重要的一點就是計算的順序。

把有限個數相加時，不管怎麼變化相加的順序，答案是不變的。例如計算 a，b，c 三個數的和，用下列六種順序計算，結果都相同。

a b c，b c a，c a b，a c b，c b a，b a c。

這個事實不僅僅對于三個數成立，甚至100個數，1000個數等，隻要是有限個數，總是成立的。

這是做加法運算時非常方便的法則。可是這個法則在無窮個數的加法運算中已經不成立，柯西以前的數學家們誰也沒有注意到這個事實。

前面已經叙述了

當決定把它分成

時，實際上已經改變了計算順序，這就是悖論産生出來的原因。如果規定這個無窮級數按照原來的排列順序相加計算，悖論就不會産生了。

上面的例子，可以計算如下：

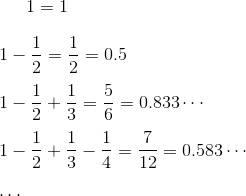
這樣計算下去，可以知道這個無窮級數的值逐漸接近In2。

如果按照這個順序計算下去，就不必擔心答案會不一樣。柯西還進一步把當時的數學家從一個迷信當中解放了出來。

這個迷信就是認為無窮級數總是有和的。這一點在有限級數中沒有什麼懷疑。例如求1000個數的和，隻要堅持不懈連續計算下去最後一定會得出正确的答案。

但無窮級數的求和運算也可能沒有答案，首先注意到這個問題的人就是柯西。

對于根本不存在的東西，若是假定它存在的話，其結果必然會引起混亂。比方說前面叙述過的波爾察諾級數就是如此，如果認為存在，則

結果得出x=1/2。根據柯西的理論，首先設x的做法就不對，答案必然不對。

由于無窮級數也可能沒有和，所以後來的數學家不必非得找個什麼理由去求和了。

柯西理會到進行無窮級數的求和運算過程中，不能随意改變相加的順序，而且也可能有的無窮級數沒有和，他還提出了與以前不同的新的想法，這就是數列的收斂和發散的概念。

設有下列無窮級數

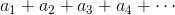
要計算這個級數，必須從左邊開始按順序地相加：

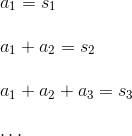
此刻，形成一列數s₁，s₂，s₃，…，像這樣按順序排列的數叫數列。根據柯西的理論，這個數列在漸漸逼近某一确定數 s 的時候，成為數列sn收斂于s，把收斂目标的數 s 稱作極限。

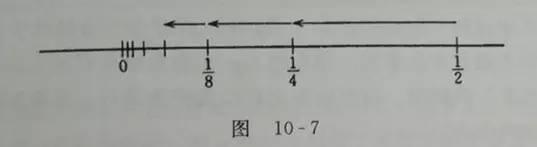
例如

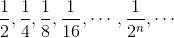
這個無窮數列逐漸接近0，所以它收斂于0，極限是0（見圖10-7）。

說到這裡可能有人認為所有的困難都已經解決了，可是還有一個問題沒有解決，那就是 "逐漸逼近s " 這句話。

* 節選自《數學與生活》10.3~10.4，作者遠山啟[日]。

點擊“閱讀原文”查看該書詳情

更多精彩资讯请关注tft每日頭條，我们将持续为您更新最新资讯!