（1）理解對數的概念及其運算性質，知道用換底公式将一般對數轉化成自然對數或常用對數；了解對數在簡化運算中的作用.

（2）理解對數函數的概念，理解對數函數的單調性，掌握對數函數圖象通過的特殊點.

（3）知道對數函數是一類重要的函數模型.

一、對數與對數運算

1．對數的概念

（2）牢記兩個重要對數：常用對數，以10為底的對數lgN；自然對數，以無理數e=2.71828…為底數的對數lnN.

2．對數的性質

3．對數的運算性質

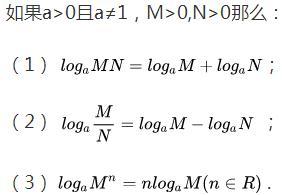
4．對數的換底公式

換底公式将底數不同的對數轉化為底數相同的對數，進而進行化簡、計算或證明.換底公式應用時究竟換成什麼為底，由已知條件來确定，一般換成以10為底的常用對數或以e為底的自然對數.

二、對數函數及其性質

1．對數函數的概念

2．對數函數的圖象和性質

一般地，對數函數 的圖象與性質如下表所示：

在直線x=1 的右側，當a>1 時，底數越大，圖象越靠近x軸；當0<a<1 時，底數越小，圖象越靠近x軸，即“底大圖低”．

3．對數函數與指數函數的關系

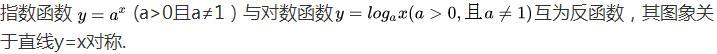
考向一 對數式的化簡與求值

對數運算的一般思路：

（1）對于指數式、對數式混合型條件的化簡與求值問題，一般可利用指數與對數的關系，将所給條件統一為對數式或指數式，再根據有關運算性質求解；

（2）在對數運算中，可先利用幂的運算性質把底數或真數變形，化成分數指數幂的形式，使幂的底數最簡，然後運用對數的運算性質、換底公式，将對數式化為同底數對數的和、差、倍數運算.

注意：

（2）注意利用等式lg2 lg5=1 .

考向二 對數函數的圖象

3．對一些可通過平移、對稱變換作出其圖象的對數型函數，在求解其單調性(單調區間)、值域(最值)、零點時，常利用數形結合思想求解．特别地，要注意底數a>1 和0<a<1 的兩種不同情況．有些複雜的問題，借助于函數圖象來解決，就變得簡單了，這是數形結合思想的重要體現．

4．一些對數型方程、不等式問題常轉化為相應的函數圖象問題，利用數形結合法求解.

考向三 對數函數性質的應用

對數函數的性質及其應用是每年高考的必考内容之一，多以選擇題或填空題的形式呈現，難度易、中、難都有，且主要有以下幾種命題角度：

（1）比較對數式的大小：

①若底數為同一常數，則可由對數函數的單調性直接進行判斷；若底數為同一字母，則需對底數進行分類讨論；

②若底數不同，真數相同，則可以先用換底公式化為同底後，再進行比較；

③若底數與真數都不同，則常借助1,0等中間量進行比較．

（2）解對數不等式：

考向四 對數函數的複合函數問題

與對數函數相關的複合函數問題，即定義域、值域的求解，單調性的判斷和應用，與二次函數的複合問題等，解題方法同指數函數類似.研究其他相關函數的單調性、奇偶性一般根據定義求解,此外，需特别注意對數函數的定義域及底數的取值.

【名師點睛】

1、利用指數函數、對數函數及幂函數的性質比較實數或式子的大小，一方面要比較兩個實數或式子形式的異同，底數相同，考慮指數函數增減性，指數相同考慮幂函數的增減性，當都不相同時，考慮分析數或式子的大緻範圍，來進行比較大小，另一方面注意特殊值 的應用，有時候要借助其“橋梁”作用，來比較大小．

判斷複合函數單調性要注意把握兩點：一是要同時考慮兩個函數的的定義域；二是同時考慮兩個函數的單調性，正确理解“同增異減”的含義（增增 增，減減 增，增減 減，減增 減）.

2、對于連等問題，常規的方法是令該連等為同一個常數，再用這個常數表示出對應的 ，通過作差或作商進行比較大小.對數運算要記住對數運算中常見的運算法則，尤其是換底公式以及0與1的對數表示.

3、比較幂或對數值的大小,若幂的底數相同或對數的底數相同,通常利用指數函數或對數函數的單調性進行比較；若底數不同,可考慮利用中間量進行比較.

更多精彩资讯请关注tft每日頭條，我们将持续为您更新最新资讯!