不确定性原理和傅裡葉變換有關？如何利用氫原子波函數驗證不确定性原理？5月8日中午12時，《張朝陽的物理課》第五十二期開播，搜狐創始人、董事局主席兼CEO張朝陽坐鎮搜狐視頻直播間，承接上一次線下課程的内容，介紹了如何基于氫原子波函數驗證測不準關系，并深入探讨了波函數在動量空間下的展開，借此解釋了不确定性原理與傅裡葉變換的關系。

測不準關系是對的嗎 氫原子波函數做驗證

在上一期的線下課中，有聽衆提問，如何通過氫原子波函數驗證測不準關系？當時張朝陽給了一個初步的解答。在本節課程中，他對這個問題作了更深入的分析。

測不準關系，或稱不确定性原理。它可以簡單表述為同時測量位置和動量時，位置的不确定度Δx和動量的不确定度Δp滿足

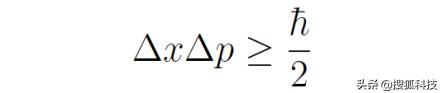
考慮到量子力學的統計诠釋，比如測量位置時，已知粒子波函數為ψ(x)，那麼在區間[x,x dx]上找到粒子的概率為

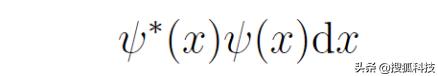
那麼Δx大約等于(位置)波函數的彌散範圍。類似地，Δp約等于波函數在動量空間展開後的彌散程度。

對于氫原子，忽略氫原子整體運動的自由度，氫原子的哈密頓算符可以寫為

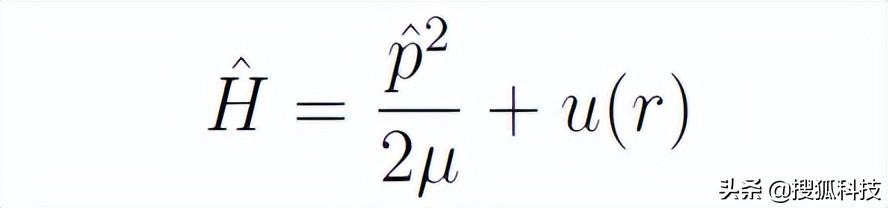
其中μ是約化質量，它和電子質量、質子質量的關系為

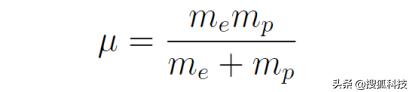
哈密頓算符中的u(r)是庫侖勢，它等于

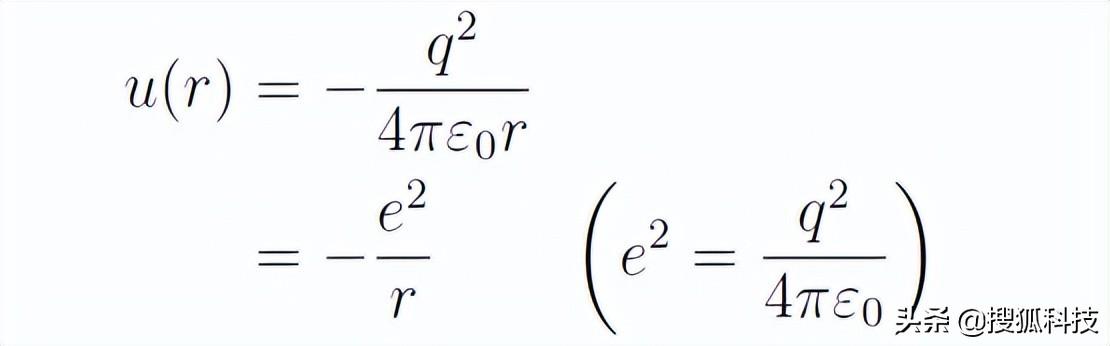
張朝陽強調，在量子力學裡人們幾乎不再使用力的概念，轉而考慮勢。在經典力學中，力正比于勢的梯度，因此無論使用力來描述還是使用勢來描述，都是等價的。隻不過由于牛頓第二定律的加持，力看起來比勢更基本。而在量子力學中起主要作用的是哈密頓算符，勢能是其中一部分，因此人們更關注勢而非力。

據悉，在下一期線下課時，張朝陽将會向大家介紹如何求解氫原子問題。在此，他直接給出了氫原子的一些結論。比如，氫原子的能級是

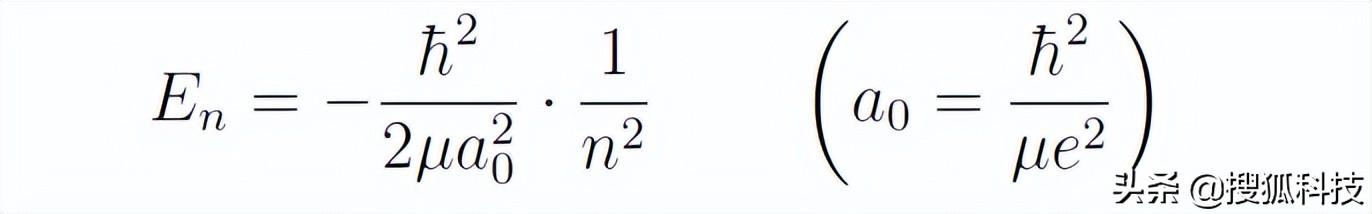
其中n取正整數值，a0是玻爾半徑。于是，氫原子的基态能量為

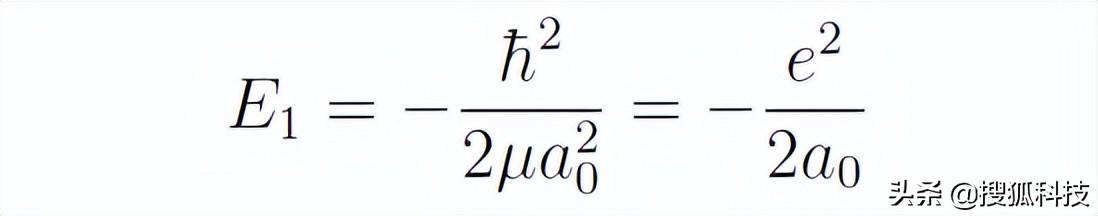
同時，張朝陽給出了氫原子基态波函數：

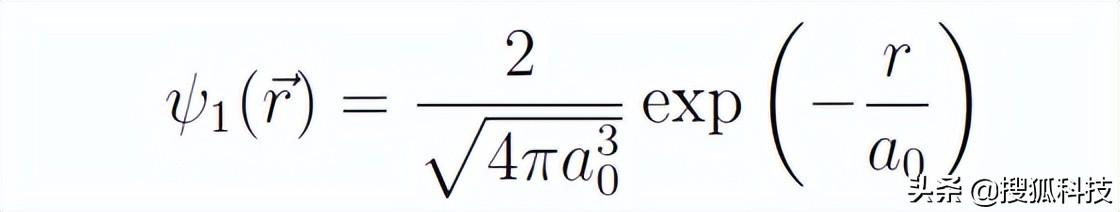
前面使用斜體字母e表示元電荷，故這裡用exp表示以自然常數e為底的指數函數，以避免混淆。上述波函數是哈密頓算符的本征函數，于是

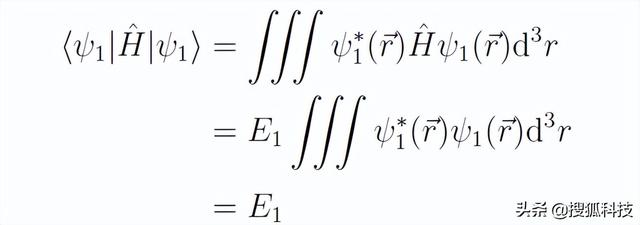
所以

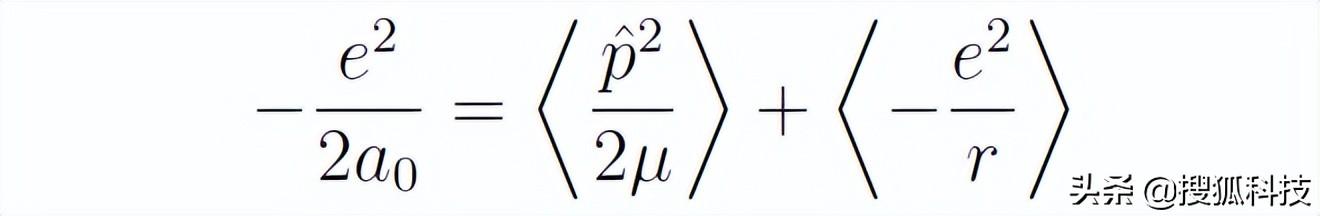
接着，張朝陽介紹怎麼計算勢能的均值。這可以通過将波函數代入得到：

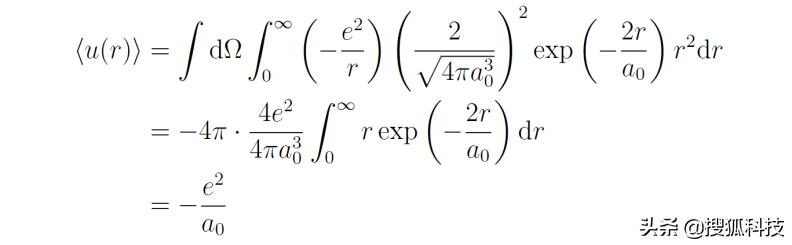
代入前面倒數第二個等式，有

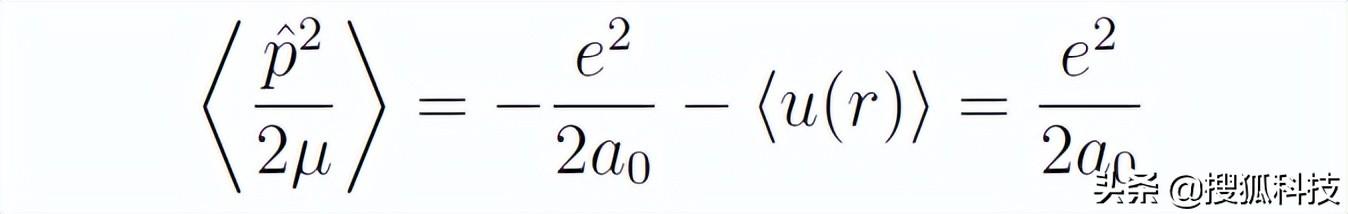
所以

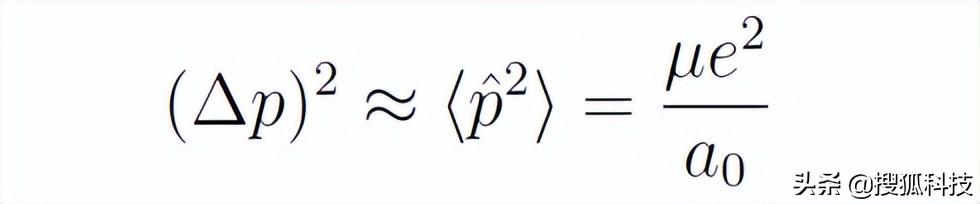
在這裡，将(Δp)^2近似為動量算符平方的均值。進一步地，由于基态氫原子的大小約等于玻爾半徑，所以

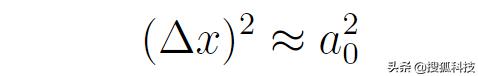
這樣就有

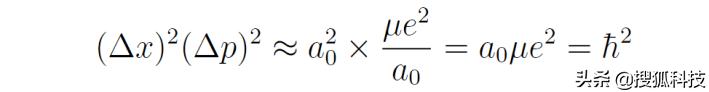
開方得到

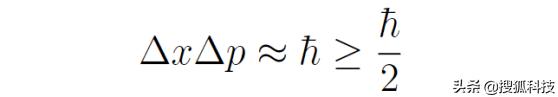
這正是張朝陽在上一期線下課所得到的結果。所以，氫原子基态滿足測不準關系，在此得到驗證。

（張朝陽驗證氫原子基态波函數滿足測不準關系）

他還介紹，對于能量和時間也有一個類似于測不準關系的式子，隻不過其中的Δt不能簡單地解釋為時間的不确定度。對于這個關系，張朝陽提了氫原子能量本征态的例子。當氫原子處于能量本征态時具有确定的能量，所以ΔE等于0。若忽略擾動，氫原子處在能量本征态上的時間為無窮大，即Δt為無窮大。

突破思維障礙 暢遊動量空間

緊接着，張朝陽介紹了波函數在動量空間下的展開。動量算符在位置空間的表達式為

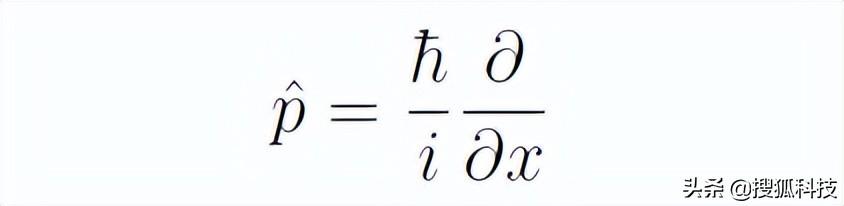
動量本征函數滿足

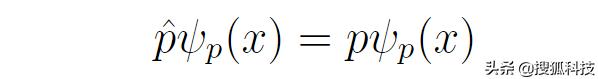
這是一個很容易求解的方程，它的解為(注：由于接下來不再用到電子電荷，所以從這裡開始用e表示自然對數之底)

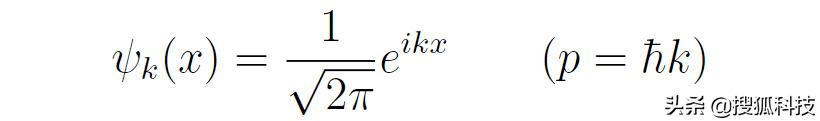
可以直接代入驗證是否滿足動量本征方程：

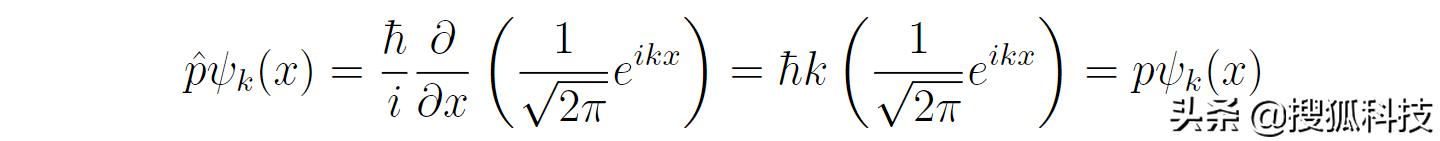
ψ_k(x)前面的系數來源于正交基的要求：

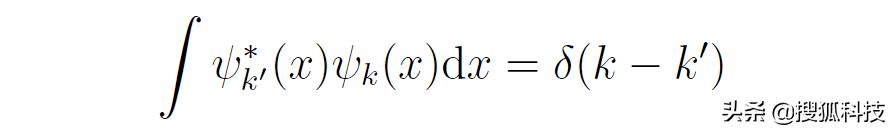
對此，張朝陽作了進一步的解釋。ψ_k(x)必然正比于e^(ikx)，假設比例系數為A。由于波函數差一個相位不影響物理結果，因此可以假設A>0。求這組基的内積，有

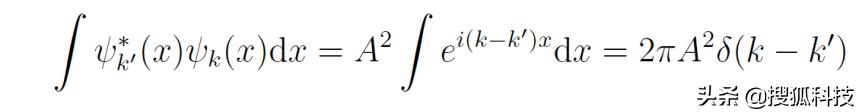
其中用到了如下數學結果：

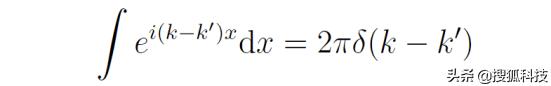
所以

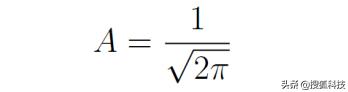
他強調，當k和k’相等時，波函數内積為無窮大。所以動量本征函數是無法歸一化的。這說明動量本征矢不是一個嚴格意義上的物理态。這是容易理解的，因為全空間的理想平面波隻是理想化的結果。實際中的物理态隻能是動量本征态的疊加，并且必然是能夠歸一化的。

張朝陽進一步介紹，對于動量本征态，它的動量是确定的，不确定度為0。而它在坐标空間卻充滿整個空間，因此位置的不确定度為無窮大。這滿足不确定性原理。

動量位置不能同時測準 兩百年前已經初現端倪

對于一般的物理态，它可以展開成動量本征态的線性疊加：

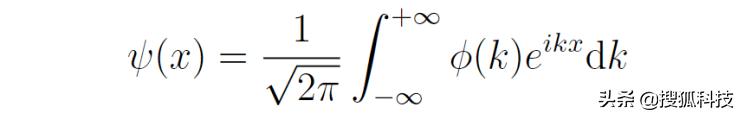
假設Ф(k)的最大值處在k0處，并且取值較大的部分集中在k0的±Δk範圍内，換言之，k的不确定度約為Δk。Ф(k)的函數圖示如下

設

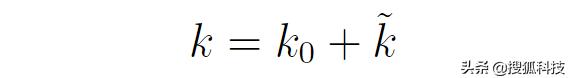
以及

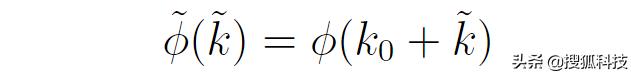
這相當于把Ф(k)的最大值平移到了原點處。于是

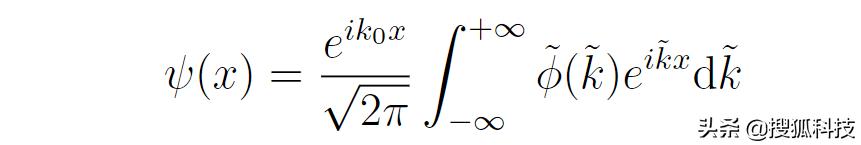
由于在最大值點的±Δk範圍外Ф(k)約等于0，所以可以将上述積分近似為

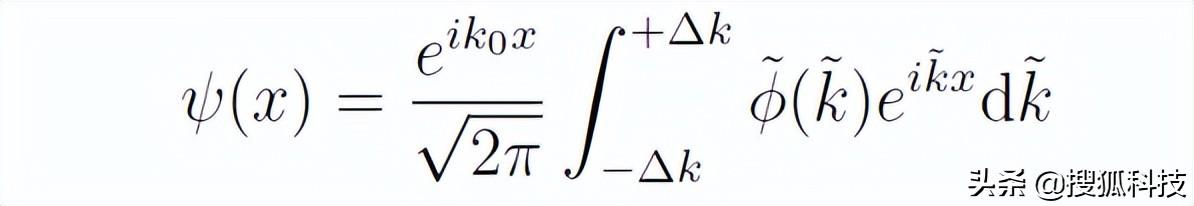
積分前面的相位可以暫時忽略。積分内的指數函數可以展開為

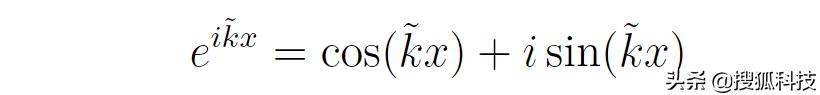
它的實部和虛部都是在-1和1之間來回震蕩的。當xΔk大于1時，積分内的指數函數會在積分區間裡快速震蕩，從而使得積分值非常小；當xΔk小于1時，積分内的指數函數比較平緩，積分值一般不接近于0。所以，位置波函數主要集中在xΔk小于1處。因為Δx衡量的是位置波函數的彌散程度，所以Δx約等于1/Δk。考慮到xΔk大于1時，波函數不是嚴格等于0，Δx有可能大于1/Δk，所以應該嚴格表述為ΔxΔk大于或者約等于1。考慮到k和動量p的關系，有

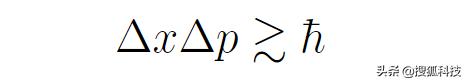
這正是位置和動量的測不準關系。

（張朝陽解釋不确定性原理和傅裡葉變換的聯系）

張朝陽對這個結果作了進一步解釋。這裡的推導隻使用波函數在動量空間的展開，而這個展開本質上是傅裡葉變換。所以說，是傅裡葉變換的性質導緻了測不準關系。傅裡葉變換和傅裡葉級數在兩百多年前就被發現了，比量子力學的提出早一百多年。那為什麼當時的人們沒能發現測不準關系呢？這是因為要想得到測不準關系，還需要把傅裡葉變換的頻率k和動量p建立起關系，并且需要量子力學的統計诠釋。

解答網友提問 探讨氫原子與能量本征态

在本期線上課程的結尾，張朝陽還與網友們進行了實時互動。對于有網友提問為什麼氫原子會處于能量本征态？張朝陽介紹，氫原子不一定都處于能量本征态，但是它的态肯定能表示成能量本征态的線性疊加。進一步地，這裡處理的氫原子模型是比較理想化的，實際上氫原子不斷受到擾動。在這些擾動下，一些原本能量較高的氫原子可能會釋放出光子并躍遷到低能态。所以，即使在某個時刻氫原子處于某個由能量本征态疊加而成的态，經過一段時間後，它都會處于某個能量本征态上，而這個能量本征态大概率是基态。

此外，對于“為什麼我們要關心能量本征态？”的問題，張朝陽解釋，任何一個可觀測量算符的本征矢都可以作為正交基，因此都可以用于态的展開，從這個角度來看，所有可觀測量都是平權的。那為什麼能量本征态要得到重視呢？淺顯地說，之所以處理能量本征态，是因為在勢場不含時的情況下，對薛定谔方程做分離變量，自然而然地會得到能量本征方程，也就是定态薛定谔方程。所以人們不可避免地要經常面對能量本征态。

但是，更值得人們深思的是，為什麼薛定谔方程的一邊恰恰是能量算符而不是其他算符？為什麼是哈密頓算符(能量算符)衡量态在單位時間内的改變量？如果用别的算符替代能量算符的作用，那麼人們需要處理的就不是能量本征态了，可見正是因為哈密頓算符出現在薛定谔方程的右邊才會導緻能量本征态的特殊性。至于為什麼恰恰是哈密頓算符，這在自然哲學的角度下是一個宏大的問題。

據了解，《張朝陽的物理課》于每周周五、周日中午12時在搜狐視頻直播，網友可以在搜狐視頻“關注流”中搜索“張朝陽”，觀看直播及往期完整視頻回放；關注“張朝陽的物理課”賬号，查看課程中的“知識點”短視頻。此外，還可以在搜狐新聞APP的“搜狐科技”賬号上，閱覽每期物理課程的詳細文章。

更多精彩资讯请关注tft每日頭條，我们将持续为您更新最新资讯!