證明ab＋cd＝ef（其中a、b、c、d、e、f為圖中已知的線段）幾何題曆來是中學數學學習中難點，面對這類問題一開始就令人覺得無從下手，或思考不了幾步便黔驢技窮，最終都不得不遺憾地放棄．

事實上這類問題的證明很簡單，隻需要遵循“截相似，證相似”即可。即在某個三角形中截取一個三角形，使它與某個三角形構成一對相似三角形，然後再證另一對相似三角形。

具體請看以下幾例．

例1　如圖1，AB是半圓的直徑，弦AC、BD相交于點E．

求證：AE·AC＋BE·BD＝AB²．

解析：首先考慮到AB為直徑，連接AD、BC，則∠C=∠D=90°。

作EF⊥AB于F，則可得兩對相似三角形，即△AEF∽△ABC，△BEF∽△BAD，

所以AE/AB=AF/AC，BE/BA=BF/BD，

所以AE·AC=AF·AB，

BE·BD=BF·BA，

兩式相加，得

AE·AC＋BE·BD＝AF·AB BF·BA=

AB（AF BF）=AB ·AB =AB²．

例2　如圖2，ABCD是圓内接四邊形．

求證：AB·CD＋AD·BC＝AC·BD（托勒密定理）．

解析：因為∠BAC=∠BDC，所以可在AC上取一點E，使△BAE∽△BDC，則

AB/BD=AE/DC，∠AEB=∠DCB，

所以AB·CD=BD·AE……（1）

因為∠AEB=∠ACB ∠EBC，

∠DCE=∠DCA ∠ACB，

所以∠EBC=∠DCA，

又∠DCA=∠ABD，

所以∠EBC=∠ABD，

又∠BCE=∠BDA，

所以△BCE∽△BDA，

所以BC/BD=CE/AD，

所以AD·BC=BD·CE……（2）

（1） （2），得

AB·CD AD·BC=BD·AE BD·CE=BD（AE CE）=BD·AC.

例3 如圖3，等腰ΔABC中，AB＝AC，D是底邊BC上任一點．

求證：AB²=AD²＋BD·DC．

解析：因為AB=AC，

所以∠B=∠C。

故在AB上取點E，使∠BDE=∠CAD，

則△BDE∽△CAD，

所以BD/AC=BE/DC，

所以BD·DC=AC·BE………（1）

因為∠AED=∠B ∠BDE，

∠ADB=∠C ∠CAD，

所以∠AED=∠ADB，

又∠DAE=∠BAD（公共角），

所以△ADE∽△ABD，

所以AD/AB=AE/AD，

所以AD²=AB·AE……（2）

（1） （2），得

BD·DC AD²=AC·BE AB·AE=AB（BE AE）=AB·AC=AB²，

所以AB²=AD²＋BD·DC．

例4（2013年全國初中數學聯賽題）如圖4，圓内接四邊形ABCD中，CB＝CD．

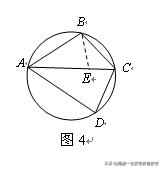
求證：CA²－CB²＝AB·AD．

證明：因為CB=CD，

所以∠BAC=∠DAC，

作∠ABE=∠DCA，BE交AC于E，

則△ABE∽△ACD，∠AEB=∠D，

所以AB/CA=AE/AD，

所以AB·AD=CA·AE……（1）

因為∠D與∠ABC互補，∠AEB與∠BEC互補，

所以∠BEC=∠ABC，

又∠BCE=∠ACB（公共角），

所以△BCE∽△ACB，

所以BC/CA=CE/BC，

所以BC²=CA·CE……（2）

（1） （2），得

AB·AD BC²=CA·AE CA·CE=CA（AE CE）=CA²,

所以CA²－CB²＝AB·AD．

更多精彩资讯请关注tft每日頭條，我们将持续为您更新最新资讯!